基于理解    突出探究   提高核心素养

－－－“合并同类项”课例研究

摘要：作者通过对两次《合并同类项》一课的展示和分析，改变了教学设计思维和理念，提出了新课程数学教学课堂的实质，揭示教学规律，对学生掌握数学知识和提高学习数学的核心素养具有启发性。

关键词： 核心素养   教学理念   内涵

正文

整式的加减运算是数与代数领域中最基本的运算，它是学生今后学习整式乘除、因式分解、分式和根式运算、方程，以及函数等知识的重要基础，而同类项及合并同类项的法则是学习整式加减法运算的基础。整式的运算与数的运算具有一致性，由于整式中的字母表示数，因此数的运算性质和运算律在式的运算中仍然成立。同类项的概念、合并同类项的法则，让学生体会数式通性，为后续数与式的学习打开思路，指明研究方法。大部分教师讲授同类项概念时，是举例归纳出概念，该教法存在的问题是学生没有经历概念的数学化过程，不能自发同化新概念，使学习流于表面化。学生只是记住教师给的定义，缺少主动思维，时间久就容易忘记。学生的问题具体表现在以下几方面：

（1）不明白为什么要给单项式分类，怎样给单项式分类；

（2）不明白为什么-5与π是同类项；

（3）学生不能很好的区分3ab²和－5a²b是不是同类项。因为学生受到了单项式的次数这一关键特征的影响。教师只是告诉学生根据定义它们不是同类项，导致学生没有理解定义的合理性。同类项概念的教学，要解决的关键问题是如何给单项式分类。

一、第一次课例展示及分析

§2.2整式的加减(第一课时合并同类项)

教学目标：

1.理解同类项的概念；掌握合并同类项的方法；

2. 经历概念的形成过程和法则的探究过程，培养观察、归纳、概括能力，发展应用意识;

3.通过类比数的运算探究合并同类项的法则，从中体会数式通性和类比的数学思想。

4.通过小组讨论、合作学习等方式，经历概念的形成过程；培养学生自主探索知识和合作交流的能力.

教学重难点：

重点：同类项的概念、合并同类项的法则及应用。

难点：正确判断同类项；准确合并同类项。

教学方法

问题引入----同类项的概念----合并同类项----整式化简求值----课堂小结----巩固练习 

教学过程：

一、创设情境一

问题1：

大家都听说过“物以类聚”吧，它的意思是同一类型的东西可以聚集在一起，当然不同类型的东西，就不能随意聚集。比如，收拾房间，书放到书架上，衣服放进衣橱，碗盘放进碗橱......

问题2：

（1）在日常生活中，你发现还有哪些事物也需要分类？能举出例子吗？如:垃圾、零钱、水果及各种产品分类.

（2）生活中处处有分类的问题，在数学中也有分类的问题吗？

目的在于引发和提高学生学习的积极性，启发学生的探索欲望，加强学科联系，并注意联系生活，同时为本课学习做好准备和铺垫。

形成概念

1.议一议: 有八只小白兔，每只身上都标有一个单项式，你能根据这些单项式的特征将这些小白兔分到不同的房间里吗？（无论你用几个房间）

10a和20a  2b² 和 6b²   -9xy和 5xy  5ab 和 -13ab　

2．思考：归为同类需要有什么共同的特征？（引导学生看书，让学生理解同类项的定义）

让学生充分发挥主体作用，从自己的视点去观察、归纳、总结得出同类项的概念。

二、观察探究，分组讨论

多媒体展示：

思考：上述代数式归为四类需要有什么共同的特征？

小组交流讨论后请学生归纳

得出同类项的概念：所含字母相同，并且相同字母的指数也相同的项称为同类项。

 所有的常数项也叫同类项。

（设计意图：教师充分发挥学生的主体作用，让学生从自己的视点去观察、归纳，让学生亲自体验知识获得的过程，享受成功的喜悦。）

三、深入思考，强化概念

思考：1.同类项的判断依据是什么？有哪几个方面？

     2.同类项与系数有关吗？

     3 .同类项与它们所含字母的顺序有关吗？

强化：1.判断下列各组中的两项是不是同类项？

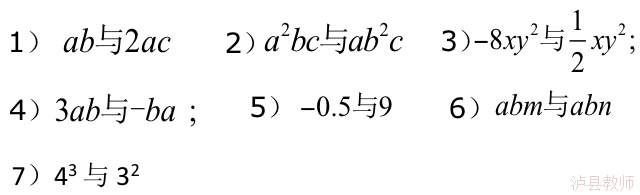
（设计意图：趁热打铁的简单练习，有利于巩固知识，使学生牢固掌握同类项的知识，增强应用意识。）

2．标出下面多项式中的同类项

（1） -3x²y + 2x²y + 3xy² - 2xy²  (2) 4x² + 2x + 7 + 3x–8x² -2

3．如果 5x³y^a和 -3x^by²是同类项，则 a =________, b=________。

设计意图：这些习题由浅入深，由易到难，先由学生完成，让学生在练中“碰壁”，从而产生困惑，再经过老师点拨，就对概念的内涵与外延都有了深刻的理解，掌握概念的本质特征，增强在不同问题情景中灵活运用概念的能力，从而突破难点——准确判别同类项

(四)   再创情境，引出法则

1.问题：两个苹果加三个苹果等于几个苹果？一个梨子加两个梨子等于几个梨子？

2a  +  3a  = 5a           b²  +  2b²  =  3b²

让学生观察等式，看有哪些发现？学生通过讨论，容易得出结论，左边两项系数之和等于右边的系数。

师：这是不是合并同类项的方法呢？这只是一个猜想，为了验证是否正确，看问题二。

出示问题2：

（1）运用运算律计算：

100×2＋252×2＝(         )×2＝________

100×（-2）＋252×（-2）＝(         )×（-2）＝________

（2）根据（1）中的方法完成下面的运算，并说明其中的道理：

100t＋252t＝(        )t＝（       ）t

3x²＋2x²＝(       )x²＝(       )x²

3ab²－5ab²＝(       )ab²＝(       )ab²

学生展开讨论，教师深入学生中间，参与学生讨论，指导学生探究，验证上述认识的正确性。

打消疑点之后，提出问题3：合并的过程中，什么变了什么没变？

有上面两个问题做基础，学生极易回答这个问题，系数变了，字母与字母的指数没变。教师抓住时机，让学生总结概括合并同类项的法则

设计意图：这样通过教师置疑、设问，引导学生经历了猜想、验证、概括的过程，使学生积极主动地探求知识与知识的发生过程，加深对知识的巩固理解。同时，也使学生感受到成功的喜悦，增强学生的自信心

归纳总结：

1.合并同类项:
‎把多项式中的同类项合并成一项就叫做合并同类项.

2.合并同类项的法则：

同类项的系数相加，所得结果作为系数，字母和字母的指数不变。

快速巩固：下列各题合并同类项的结果对不对？若不对，请改正。

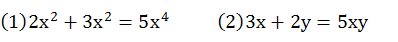
同类项，须判断，两相同，是条件 ；合并时，须计算，系数加，两不变 。

（设计意图：以口诀的形式巩固法则通俗易记，朗朗上口，增强学生学习的趣味性。）

（五） 例题分析，合作交流

例1：合并下列多项式中的同类项：





例2：化简多项式

（设计意图：教师示范解题格式，规范操作，学生再加以运用，注重培养学生规范解题的能力。）

（六）练习巩固，强化目标

1.下列各题中的两项是不是同类项？

2.判断下面合并同类项是否正确，若有错，请改正：

3.合并下列各式中的同类项：

4.整式化简：

(七)小结与评价

在课堂临近尾声时，请学生谈一谈:通过本节课的学习，学会了那些知识；掌握了那些学习数学的方法。（学生畅所欲言）

设计意图:培养学生归纳和语言表达能力，鼓励学生从数学知识、数学方法和数学情感等方面进行自我评价。

（八）作业布置：

必做题：P65第2题，P70第5题    

选做题：P70第4题，P71第11题

设计意图：必做题巩固所学知识，查找学习中的漏洞和不足，课后进一步完善补充；布置选做题，让学有余力的学生进一步发展思维、培养能力。

教学设计理念：本节课是在学习了单项式、多项式之后，以同类项的概念、合并同类项的法则及其运用为教学内容。合并同类项是本章的一个重点，其法则的应用是整式加减的基础，也是以后学习解方程、解不等式的基础。另一方面，这节课与前面所学的知识有着千丝万缕的联系：合并同类项的法则是建立在数的运算的基础之上；在合并同类项过程中，要不断运用数的运算。可以说合并同类项是有理数加减运算的延伸与拓广。因此，这是一节承上启下的课。

二、第二次课例展示及分析

§2.2整式的加减(第一课时合并同类项)

教学目标：

1.理解同类项的概念；掌握合并同类项的方法；

2. 经历概念的形成过程和法则的探究过程，培养观察、归纳、概括能力，发展应用意识;

3.通过类比数的运算探究合并同类项的法则，从中体会数式通性和类比的数学思想。

4.通过小组讨论、合作学习等方式，经历概念的形成过程；培养学生自主探索知识和合作交流的能力.

教学重难点：

重点：同类项的概念、合并同类项的法则及应用。

难点：正确判断同类项；准确合并同类项。

教学方法

问题引入----同类项的概念----合并同类项----整式化简求值----课堂小结----巩固练习 

教学过程：

一、创设情境

问题1：

师：在上次“送温暖，献爱心”班级主题活动中，我们班上同学非常积极，为班上家庭困难的同学捐款，现在我把所有捐款的钱拿出来了，纸币有一元、有伍元、有拾元，你们能以最快的方式统计一下共有多少钱吗？

生：一名学生上台来，把钱按照一元、伍元，拾元进行分类，然后进行汇总计算。

问题2：

.师：谢谢你。你为什么这样整理呀？

生：因为这些纸币一共有三种面值，我按面值将它们进行了分类，把同一种面值的纸币放在一起，用面值去乘以张数再相加就是总数。

问题3.

师：老师手里有三种不同颜色的花，现在我要把这三束鲜花随意组合成两束鲜花。

议一议:

1.师：若一枝红玫瑰的价格是 a 元，一枝黄玫瑰的价格是 b 元，一枝香水百合的价格是c 元。根据这些已知条件及实物，你可以求出些什么？

生：根据这些条件及实物，我可以知道这两束鲜花中三种不同颜色的鲜花的总价分别是多少？

2．师：很好。我们就来研究这个问题 ----这两束鲜花中红玫瑰的总价是多少？哪个同学能用代数式把它表示出来？如何计算？

生 1 ：我认为红玫瑰的总价是 5a 元。

生 2 ：我认为也可以用 2a+3a 表示。

生 3 ：也可以用（ 2+3 ） a 表示。

师：  根据学生的回答教师及时板书 2a+3a= （ 2+3 ）a=5a

3.师：刚才有几位同学说出了自己的答案，我想问从第二个式子变到第三个式子，运用了什么知识？

生：乘法分配律

4.同学们，你能算一下第一束鲜花的总价是多少吗？

生：可以用2a+3b+c来表示

师：请问上面两个式子2a+3a 与2a+3b+c有什么不同？

生：第一个式子含有相同的字母，他们是同类；第二个式子的字母不相同，他们不是同类。

5.师：归为同类需要有什么共同的特征？（引导学生看书，让学生理解同类项的定义）

设计意图：从生活导入，使学生体会分类、合并的思想方法在现实生活中的实际意义，体现数学来源于生活又服务于生活的思想。

二、观察探究，分组讨论

多媒体展示：

（1）2t;   (2)10;    (3)4ab;    (4)-12t;   (5)2a²b;     (6)6ab;      (7)-3;    (8)-7ba;    (9)-5a²b;  (10)-t;  

(11)π      (12)-8ba²

思考：请同学们对以上单项式进行分类，并说明分类的依据。

小组交流讨论后请学生归纳

（1）10，-3，π；(2)2t，-12t，-t；(3)4ab，6ab，-7ba；(4)2a²b，-5a²b，-8ba²

师：为什么第（3）类的单项式能归为一类？

生：因为他们含有相同的字母。

师：那么第（3）和（4）所含的字母也相同，为什么他们不归为一类呢？

生：虽然他们的字母相同，但是字母的指数不一样。

师追问：单项式2a²b和-3ab²是同类吗？说说你的看法。

生：这两个单项式的字母相同，指数一样，但是相同字母的指数不一样。

师：为什么2a²b，-5a²b，-8ba²能归为一类？

生：他们所含字母相同，并且相同字母的指数也相同，只是顺序不一样。

得出同类项的概念：所含字母相同，并且相同字母的指数也相同的项称为同类项。

教师强调：1. 所有的常数项也叫同类项。2.“两相同”即所含字母要相同，相同字母的指数也要相同

设计意图：教师鼓励学生从不同角度去归类，然后重点分析同类项的方式进行归类；充分发挥学生的主体作用，让学生从自己的视点去观察、辨析、交流，归纳，让学生亲自尝试给单项式分类，更深刻理解同类项的概念，体验知识获得的过程，享受成功的喜悦。

三、深入思考，强化概念

思考：1.同类项的判断依据是什么？有哪几个方面？

     2.同类项与系数有关吗？

     3 .同类项与它们所含字母的顺序有关吗？

强化：1.判断下列各组中的两项是不是同类项？

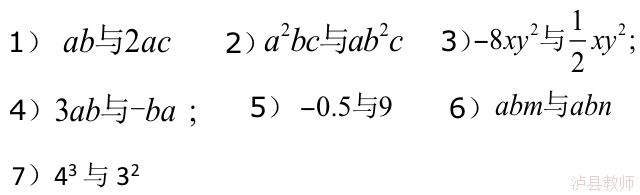
2．标出下面多项式中的同类项

（1） -3x²y + 2x²y + 3xy² - 2xy²    

（2） 4x² + 2x + 7 + 3x–8x² -2

3．如果 5x³y^a和 -3x^by²是同类项，则 a =________, b=________。

设计意图：这些习题由浅入深，由易到难，先由学生完成，让学生在练中“碰壁”，从而产生困惑，再经过老师点拨，就对概念的内涵与外延都有了深刻的理解，强化同类项的基本特征即“两相同”和“两无关”。

(四)   再创情境，引出法则

1.问题：两个苹果加三个苹果等于几个苹果？八个梨子减两个梨子等于几个梨子？

2      +3       =(    )        8      —2     =（   ）

2.师：如果把苹果和梨换成字母，又该如何计算？

2a  +  3a  =          a       b²  +  2b²  =           b²

让学生观察等式，看有哪些发现？

生：学生通过讨论，容易得出结论，左边两项系数之和等于右边的系数。

师：这是不是合并同类项的方法呢？这只是一个猜想，为了验证是否正确，看问题2。

出示问题2：

（1）运用运算律计算：

100×2＋252×2＝(         )×2＝________

100×（-2）＋252×（-2）＝(         )×（-2）＝________

（2）根据（1）中的方法完成下面的运算，并说明其中的道理：

100t＋252t＝(        )t＝                              

3x²＋2x²＝               ＝                      

3ab²－5ab²＝                                    

学生展开讨论，教师深入学生中间，参与学生讨论，指导学生探究，验证上述认识的正确性。

提出问题3：合并的过程中，什么发生了变化，什么没变化？

有上面两个问题做基础，学生极易回答这个问题，系数变了，字母与字母的指数没变。教师抓住时机，让学生总结概括合并同类项的法则

设计意图：这样通过教师置疑、设问，引导学生经历了猜想、验证、概括的过程，使学生积极主动地探求知识与知识的发生过程，加深对知识的巩固理解。同时，也使学生感受到成功的喜悦，增强学生的自信心。

归纳总结：

1.合并同类项:
‎把多项式中的同类项合并成一项就叫做合并同类项.

2.合并同类项的法则：

同类项的系数相加，所得结果作为系数，字母和字母的指数不变。

快速巩固：下列各题合并同类项的结果对不对？若不对，请改正。

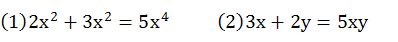
同类项，须判断，两相同，是条件 ；合并时，须计算，系数加，两不变 。

设计意图：以口诀的形式巩固法则通俗易记，朗朗上口，增强学生学习的趣味性简称为“一加两不变”。

（五） 例题分析，合作交流

例1：合并下列多项式中的同类项：

(1)    

(2)

师生共同完成例1，学生先发表自己的观点，教师板书合并同类项的一般步骤：

1.找同类项，用相同的线画出来；

2.把同类项移到一起，移项时要连同它的符号一起移；

3.合并同类项；

4.单独的项写在最后。

例2：化简多项式

生：先单独完成，再小组交流评价。

设计意图：教师示范解题格式，规范操作，学生再加以运用，注重培养学生规范解题的能力。

（六）练习巩固，强化目标

1.下列各题中的两项是不是同类项？

2.判断下面合并同类项是否正确，若有错，请改正：

3.合并下列各式中的同类项：

4.整式化简：

设计意图：通过练习强化同类项的概念，进一步掌握合并同类项的法则。

(七)小结与评价

通过本节课的学习，请学生谈一谈:

（1）学会了那些知识？

（2）掌握了那些学习数学的方法。

（3）你对自己本节课的表现有何评价？

（4）你对本节课还有哪些困惑和建议？

设计意图:培养学生归纳和语言表达能力，鼓励学生从数学知识、数学方法和数学情感等方面进行自我评价。

（九）作业布置：

必做题：P65第2题，P70第5题    

选做题：P70第4题，P71第11题

设计意图：必做题巩固所学知识，查找学习中的漏洞和不足，课后进一步完善补充；布置选做题，让学有余力的学生进一步发展思维、培养能力。

教学设计理念：本节课是在学习了单项式、多项式之后，以同类项的概念、合并同类项的法则及其运用为教学内容。合并同类项是本章的一个重点，其法则的应用是整式加减的基础，也是以后学习解方程、解不等式的基础。另一方面，这节课与前面所学的知识有着千丝万缕的联系：合并同类项的法则是建立在数的运算的基础之上；在合并同类项过程中，要不断运用数的运算。可以说合并同类项是有理数加减运算的延伸与拓广。因此，这是一节承上启下的课。

三、两次授课分析

授课教师先后在不同班级两次执教“合并同类项”一课。第一次课由授课教师自己备课、上课。经过课后与数学组成员简要讨论，授课教师简单修改教学设计，第二次在另一个班继续上课。第二次课主要是检验讨论时给出的教学建议的有效性与针对性。

第一次授课问题探讨 

第一次课存在的问题是缺少了同类项概念的生长点。学生只是在教师的引导下，形式化地得出同类项概念，然后在定义指引下做出判断。由于没有经历将单项式分类的过程，有些学生判断错误。不能正确理解同类项的定义 

第二次授课问题探讨

第二次课确立了同类项概念的生长点，学生体会到了同类项概念是单项式分类的结果，初步解决了第一次课中出现的问题。学生在整式加减运算启发下，通过字母代替数，把整数加减变为整式加减运算，经历了一般化、符号化、结构化过程，为代数式的其他运算奠定了延伸点。在教师的指导下，以贴近现实生活的问题情境引入本课无疑会提起学生极大的兴趣，激发他们潜在的强烈的求知欲，并能抓住契机引导学生认真观察，联系前面的知识，在运用知识的基础上层层深入揭示同类项的内涵，总结归纳合并同类项的法则，再通过练习巩固知识的应用。学生尝试给单项式分类，理解了同类项概念，渗透数式通性的核心思想，凸显数学抽象的核心素养。

四、教学启示

梳理上述课例研究，我们可以发现，代数思维关键特征是抽象化、一般化。初中代数的思维的关键节点是由数到式的抽象，关键教学策略就是由数到式的纵向数学化。为了帮助学生由数抽象出式，初步学会代数思维，需要采用三种教学理念。

（1）创设问题情境，化归概念本质。七年级学生一般都具有好奇、好问的探究心理，创设问题情境，能够使学生的学习心理迅速地由抑制到兴奋，而且还会使学生把知识的学习当作一种自我需要，能引起学生内部认知矛盾的冲突，使学生在疑中生奇，疑中生趣，不断激起学生的学习欲望。本节案例第二次授课中，教师创设了学生十分感兴趣的问题情境，由此使学生产生了强烈的求知欲望和主动探索的兴趣，让学生在讨论、辨析、交流、总结中突出同类项的归类，得到同类项的概念。

（2）有效组织合作探究，揭示法则规律内容。

在新课程改革中，教师不再是课程的执行者，而是课程的设计者、实施者、评价者。第二次授课中，为了学生能够自行得出并掌握合并同类项的法则，教师从简单易懂的知识入手，设计出了一系列贴近学生生活的练习，为法则的形成做好铺垫，很好地突破难点。从数到式，说明其生长点，涉及到学生的思维形式从具体思维向形象逻辑思维的过渡，铺垫出式及其运算知识的延伸点，指引学生的学习思路。

（3）重视“四基”，提高核心素养。本节课让学生经历知识的形成与应用，在学习过程中去体验数学和经历数学，教会学生基本知识、基本技能的同时，更重视对学生基本思想、基本活动经验的训练。第二次授课中立足于知识的生长点，作好启发的思路，诱导学生尝试自主完成由数到式的纵向数学化，再生知识，掌握知识的本质与规律，体验新知识的启发性、可理解性与合理性，提高学习数学的核心素养。