立足问题分析 寻求解决方法

            ——以“角”的计算教学为例

【论文摘要】“几何图形初步”的学习，学生很不适应，教师要放慢脚步，本文以“几何图形初步”中“角”的计算为例，立足问题，分析原因，寻求方法。

    【关键词】问题分析   追根溯源    

     【正文】

 七年级数学第四章“几何图形初步”既有“形”、也有“数”，学生仅仅靠记住知识是没有用的。它对学生思维能力的要求会高一些，关键是让学生建立起掌握几何概念、图形、语言、推理、思维的学习方法和学习习惯，“几何图形初步”的学习，学生很不适应，教师要放慢脚步，本文以“几何图形初步”中“角”的计算为例，立足问题，分析原因，寻求方法。

一、课本习题   发现问题

（人教版七年级数学第四章复习题4第12题p149）

如图，长方形纸片ABCD，点E，F分别在边AB，CD上，连接EF，将∠BEF对折，点B落在直线EF上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN，求∠NEM的度数.

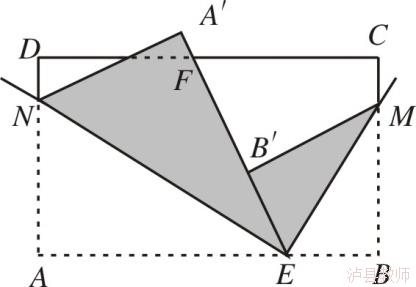
这是一道综合运用题，中档难度，题目中考查到了角的和差、角平分线的性质等知识，这些知识是第四章《几何图形初步》中的重点基础内容，是以后图形与几何学习必备的基础知识。2019年秋期选此题作为期末测试题，本题满分8分，而平均得分只有2.96分，得分率只有37%，可见学生对该部分知识掌握的不好。与考前对学生的预期差距比较大，重点的知识重点的方法重点的授课，但是学生并没有感受到它们的“重点”，或者他们承受不起这样的“重点”。重要基础内容学生掌握不好，势必影响今后图形与几何部分的学习，不利于学生数学知识的发展。

二、反思教学，分析问题

《课程标准(2011年版)》中的数学课程目标由“双基”改为“四基”即:基础知识、基本技能、基本思想和基本数学活动经验。本题涉及到的知识是最为基本核心的知识，在平时讲授中是第一时间要让学生理解和接受的。学生可能已经掌握了基础知识，已经训练了基本技能，但是有没有领悟到数学基本思想?有没有积累到数学基本的活动经验?这些是值得推敲的。本题中涉及到的数学思想方法很丰富，有数学抽象、逻辑推理、直观想象、数形结合等。

在《课程标准(2011年版)》提出了10个核心概念:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识。本题中涉及到的核心概念有符号意识、空间观念、几何直观、推理能力等。但由于学生对基础知识和基本技能没能牢固掌握，导致不会有数学思想和数学方法的准确、迅速和灵活的应用。由于没有积累数学活动经验，那么遇到陌生的问题就不会去分析，去推理，去探究。

三、追根溯源，寻求方法

学生掌握基础知识和基本技能是领悟数学思想方法和积累数学活动经验的前提，但这不是后二者的全部。《课题标准（2011年版）》指出：“数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括”。也指出：“学生积累数学活动经验是不断经历、体验各种数学活动过程的结果”。因此在学习图形与几何的过程中，基础知识的学习很重要，它是“根”和“源”，是由它们派生出了一个个心得知识点。但是，仅仅掌握好基础知识是不够的，必须通过一定量的应用训练，才能做到深刻理解，从而达到学以致用的目的。我们这里的“追根溯源”，便是达到上述目的最佳方法和途径。

1.掌握几何语言的书写，能够规范表达“几何过程”。

如：如图，OC是∠AOB的平分线

几何语言：∵OC是∠AOB的平分线

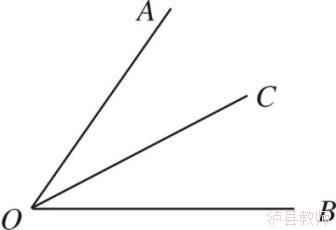
∴∠AOC=∠BOC=∠AOB

(或∠AOB=2∠AOC=2∠BOC)

像上面的几何语言是书写几何过程中的基本“素材”。只有对每一个条件和结论能够正确规范地写下来，才能确保几何题目的解题过程正确。

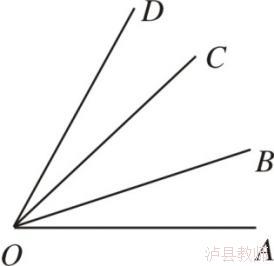
2.学会识图，从不同角度观察图形的构成。

如图，（1）∠AOC是哪两个角的和？

（2）∠AOB是哪些角的差？

角的和差是基础知识，在课堂教学时要让学生自己去观察图形，自己去体会图形的构成，从多个角中找到需要的角的组合。

3.注重一题多解，从不同的角度锻炼学生的思维。

如图，AB为一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=∠BOD，∠COE=70°，求∠EOB的度数。

本题应用方程的思想，在设未知数，以及找等量关系时方法比较多，可以让学生从不同的角度设未知数，用不同的关系表示角，找等量关系列方程求解。

4.学会画图，让教学过程更加直观化。

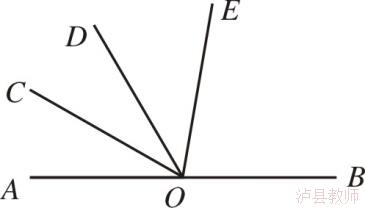
已知∠AOB=40°，自O点引射线OC，若∠AOC=30°，求OC与∠AOB的平分线OD所成的角的度数.

没有图形时要画图，图形不全时也要画图。在日常教学中要让学生体会到画图可以把问题、计算和证明变得直观：对理解概念、寻求解题思路上面带来便捷。本题没有图形，要解决本问题，需要画图；本题是多解的题目，让学生自己画图，可以在数学活动中训练到思维的严密性，积累到活动经验。

5.提炼基本图形，提高解题效率

对复杂图形进行合理分离出基本图形，然后根据基本图形去分析，可以为学生寻找解题的突破口提供线索，可以有效防止无关信息干扰，快速凸显解题突破口，提高结题效率和数学思维能力。

如图所示，已知O是直线AB上一点，∠BOE=∠FOD=90°，OB平分∠COD

（1）图中有∠DOE互余的角是      .

（2）图中是否有与∠DOE互补的角？如果有，直接写出全部结果；如果没有，说明理由。

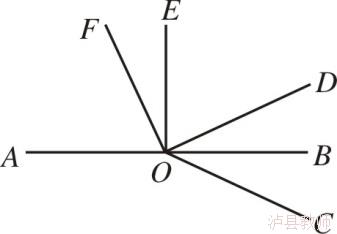
针对本题，如图所示，已知O是直线AB上一点，∠BOE=∠FOD=90°，这个图就是一个基本图。

几何教学中很多性质和定理，与它们相关的图形很多是比较典型的基本图形。熟练掌握这些图形，不断强化对这些图形的运用，会对我们识图和解题带来便捷的效果。基本图形在几何题目中应用很广泛,在教学中让学生掌握一些重要的基本图形是教学应关注的目标。

图形与几何部分的教学是一项长期的过程，教师要立足问题，借助于“形”去观察，借助于“数”去思考，通过观察、猜测、推理、反思、总结、归纳等，准确定位，寻求解决问题的方法，培养学生数学思想和数学方法，提升学生的思维品质和思维能力。

参考文献：

1.义务教育数学课程标准（2011年版）

2.童常健.突出问题本质，提升学生思维[J].中小学数学（初中版），2017(7、8):31.