泸县2021年春期期末七年级教学质量检测

数 学 试 题

全卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。全卷满分100分。考试时间共90分钟。

注意事项：

1．答题前，请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。考试结束，将试卷和答题卡一并交回。

2．选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目的答案标号涂黑。如需改动，用橡皮擦擦净后，再选涂其它答案。非选择题须用0.5毫米黑色墨迹签字笔在答题卡上对应题号位置作答，在试卷上作答无效。

第Ⅰ卷（选择题  共24分）

一、选择题（本大题共12个小题，每小题2分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）．

1．5的平方根是

A． B． C． D．

2．在实数，，，0，，中，无理数有

A．2个 B．3个 C．4个 D．5个

3．如图，点A处的轮船位于航标灯点O的方向是

A．南偏东35° B．北偏西65° C．南偏东65° D．南偏西65°

4．在下列调查中，适宜采用全面调查的是

A．了解我省中学生的视力情况 B．了解一批电灯泡的使用寿命

C．了解一批袋装食品是否有防腐剂 D．了解某班学生校服的尺码情况

5．若，则下列不等式正确的是

A． B． C． D．

6．空气是由多种气体混合而成的，为了简明扼要地介绍空气的组成情况，较好地描述数据，最适合使用的统计图是

A．扇形图 B．条形图 C．折线图          D．直方图

7．如图，我们将剪刀的两边抽象为两条直线AB与CD，它们相交于点O，若∠1=35°，则∠2=

A．30° B．35° C．40° D．45°

8．已知是方程的解，则m的值是

A．－1 B．1 C．－2 D．2

9．如图，某同学的家在P处，他想尽快赶到附近公路边搭顺风车，他选择P→C的路线，用几何

知识解释其道理正确的是

A．两点确定一条直线 

B．垂线段最短 

C．两点之间线段最短 

D．经过一点有无数条直线

10．由方程组可得出x与y之间的关系是

A． B． C． D．

11．比较实数，，的大小关系，正确的是

A． B．  C．  D．

12．在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”（用a表示）：任意两点横坐标差的最大值，“铅垂高”（用h表示）：任意两点纵坐标差的最大

值，“矩面积”用S表示，则S=ah．例如：三点坐标分别为A（1，2），B（－3，1），C（2，

－2），则a=5，h=4，S=ah=20．若D（1，2），E（－2，1），F（0，t）三点的“矩面积”为18，则t的值为

A．－3或6B．－3或7 C．－4或6 D．－4或7

第Ⅱ卷（非选择题  共76分）

注意事项：用0.5毫米黑色墨迹签字笔在答题卡上对应题号位置作答，在试卷上作答无效．

二、填空题（本大题共4小题，每小题3分，共12分）．

13．二元一次方程组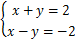的解是  ▲  ．

14．如图，直线a，b被直线m所截，若a∥b，∠2=62°，则∠1的度数是  ▲  ．

15．上课间操时，小华、小军、小刚的位置如图所示．小军问小华：“如果我的位置用（0，0）表示，小刚的位置用（2，2）表示，那么你的位置应该怎样表示？”小华的正确回答应该是  ▲  ．

16．已知关于x的不等式组只有三个整数解，则的取值范围是  ▲  ．

三、本大题共3个小题，每小题6分，共18分．

17．计算：．

18．解方程组：．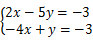

19．如图，在平面直角坐标系中，三角形ABC的顶点A，B，C的坐标分别为（0，3），（－2，1），（－1，1），把三角形ABC先向右平移2个单位长度，再向下平移2个单位长度，得到三角形， 

点，，分别为点A，B，C的对应点．

（1）在图中画出三角形，并写出点，的坐标；

（2）求三角形的面积．

四、本大题共2个小题，每小题7分，共14分．

20．解不等式组：．

21．某中学学生会为了解本校学生喜欢球类活动的情况，随机抽取了若干名学生进行问卷调查（要求每位学生只能填写一种自己喜欢的球类），并将调查的结果绘制成如下图所示的两幅不完整的统计图．

请根据图中提供的信息，解答下列问题：

（1）参加调查的学生共有多少人？

（2）将条形统计图补充完整；

（3）若该校有1500名学生，则喜欢篮球的约有多少人？

五、本大题共2个小题，每小题7分，共14分．

22．填空，完成下面的说理．

如图，AC⊥BC，DG⊥AC，垂足分别为点C，G，∠1=∠2．

试说明：CD∥EF．

解：因为 AC⊥BC，DG⊥AC，（已知）

所以 ∠DGA=∠BCA=90°，（　              　）

所以 　     　∥　     　（　                        　）

所以 ∠2=∠BCD，（　                            　）

又因为 ∠1=∠2，（已知）

所以 ∠1=∠　    　，（等量代换）

所以 CD∥EF．（　                              　）

23．如图，直线AB∥CD，直线EF分别交AB，CD于点E，F，FH平分∠EFD，如果∠1=108°，求∠2的度数．

六、本大题共2个小题，每小题9分，共18分．

24．现有A，B两种商品，买2件A种商品和1件B种商品用了90元，买3件A种商品和2件B种商品用了160元．

（1）求A，B两种商品每件各是多少元？

（2）如果小亮准备购买A，B两种商品共10件，总费用不超过350元，且不低于300元，问有几种购买方案？哪种方案费用最低？

25．已知AB∥CD，点C在点D的右侧，∠ABC，∠ADC的平分线交于点E，∠ADC=80°．

（1）如图1，当点B在点A的左侧时，

①求∠EDC的度数；

②若∠ABC=40°，求∠BED的度数；

（2）如图2，将线段BC沿DC方向平移，使得点B在点A的右侧，其它条件不变，若∠ABC=n°，求∠BED的度数（用含n的式子表示）．

泸县2021年春期期末七年级教学质量检测

数学参考答案及评分意见

一、选择题：（每小题2分，共24分）

二、填空题：（每小题3分，共12分）

13．；  14．118°；  15．（－2，－1）；   16．．

三、解答题（每小题6分，共18分）

17．解：

3分

4分

6分

18．解：，

①×2+② 得：－9y=－9，

解得y=1，2分

把y=1代入②得

x=1，4分

所以方程组的解为．6分

19．解：

（1）如图，三角形即为所求，2分

点（2，1），点（1，－1）；4分

（2）三角形的面积                    

．6分    

四、解答题（每小题7分，共14分）

20．解：

解不等式①，得

．3分

解不等式②，得

．6分

把不等式①②的解集在数轴上表示出来为

所以原不等式组的解集为．7分

21．解：

（1）参加调查的学生共有60÷20%=300（人）；2分

（2）300－120－60－30=90（人），喜欢足球的人数为90人，如图；4分

（3），喜欢篮球的人数约为600人．7分

五、解答题（每小题7分，共14分）

22．解：

因为 AC⊥BC，DG⊥AC，（已知）

所以 ∠DGA=∠BCA=90°，（垂直的定义）1分

所以  DG ∥ BC （同位角相等，两直线平行）4分

所以 ∠2=∠BCD，（两直线平行，内错角相等）5分

又因为 ∠1=∠2，（已知）

所以 ∠1=∠ BCD ，（等量代换）6分

所以 CD∥EF．（同位角相等，两直线平行）7分

23．解： 

因为 AB∥CD，

所以 ∠1+∠EFD=180°，∠2=∠HFD，2分

因为 ∠1=108°，

所以 ∠EFD=72°，3分

因为 FH平分∠EFD 

所以 ∠HFD=∠EFD=×72°=36°5分

所以 ∠2=36°．7分

六、解答题（每小题9分，共18分）

24．解：

（1）设A种商品每件为x元，B种商品每件为y元．由题意可得，

，2分

解得 4分

答：A种商品每件为20元，B种商品每件为50元．

（2）设购买A种商品a件，则购买B种商品（10－a）件，

由题意可得：，6分

解得 8分

方案1：购买A种商品5件，B种商品5件；

方案2：购买A种商品6件，B种商品4件．

答：有两种购买方案，其中方案2费用最低．9分

25．解： 

（1）①如图1，因为 ∠ADC=80°，DE平分∠ADC，

所以 ．2分

②如图1，过点E作直线MN∥AB．

因为 BE，DE分别平分∠ABC，∠ADC，

所以 ∠ABE=∠ABC=20°，∠EDC=∠ADC=×80°=40°．4分

因为 AB∥CD，MN∥AB，

所以 MN∥CD∥AB，

所以 ∠MED=∠EDC=40°，∠BEM=∠ABE=20°，5分

所以 ∠BED=∠BEM +∠MED=60°．6分

（3）如图2，过点E作直线PQ∥AB．

因为 BE，DE分别平分∠ABC，∠ADC，

所以 ∠ABE=∠ABC=，∠EDC=∠ADC=×80°=40°．7分

因为 AB∥CD，PQ∥AB，

所以 PQ∥CD∥AB，

所以 ∠PED=∠EDC=40°，∠ABE+∠BEP=180°， 

所以 ∠BEP=180°－，8分

所以 ∠BED=∠BEP+∠PED

=180°－+40°

=．9分