《图形的旋转》教学设计

泸县二中外国语实验学校    马玲

【教学目标】

知识目标：（1）理解旋转概念，会找出旋转三要素和对应点、对应线段、对应角；

（2）探索和发现旋转的相关性质；

（3）能够通过旋转的性质解决问题及做简单的旋转图形．

能力目标：通过观察、操作、交流、归纳等过程，培养学生的动手能力、观察能力、探究问题的能力以及与人合作交流的能力．经历探索图形在旋转变换中的变化情况的过程，体会旋转变换对研究图形变化的重要性．

情感目标：经历对生活中旋转图形的观察、讨论、实践操作，使学生充分感知数学美，培养学生学习数学的兴趣和热爱生活的情感；通过小组合作交流活动，培养学生合作学习的意识和研究探索的精神．

【学习重难点】

重点：旋转相关概念以及性质；

难点：利用性质作旋转图形．

【导学过程】 

还记得泸州酒城乐园吗？这节课老师就带大家去游乐园去转一转．视频引入，让学生动起来亲身体会旋转现象．

设计意图：激发学生的学习热情，引出课题《图形的旋转》．                                    

探究一: 旋转的概念

视频学习，让学生通过视频掌握旋转的定义及相关概念．

设计意图：更形象的理解旋转的概念及三要素．

　　旋转的概念: 把一个图形绕着某一定点O沿某个方向转动一个角度的图形变换叫做旋转．这个定点O叫旋转中心，转动的方向叫做旋转方向 ，转动的角叫做旋转角．如果图形上的点A经过旋转变为点A′，那么这两个点A和A′ 叫做这个旋转的对应点．

因此，旋转的三要素是________、________和_________．                          

练习：

1.下列现象中属于旋转的有 (         )个．

　　①地下水位逐年下降 ；  ②传送带的移动 ；  ③方向盘的转动；

   ④水龙头的转动；       ⑤钟摆的运动；     ⑥荡秋千.

　　 A.2         　　　  B.3       　     C.4     　　        D.5  

2.如图,△ABO 绕点O旋转得到△CDO,则:

　　　旋转中心是________；

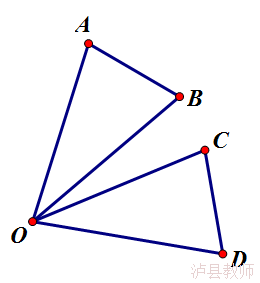
旋转方向是________________；

旋转角是_________________；

点B 的对应点是________；

线段OB 的对应线段是________；

线段CD 的对应线段是________；

∠AOB 的对应角是________；

∠B 的对应角是________．

设计意图：通过问题巩固旋转中的相关概念．

探究二：旋转的基本性质

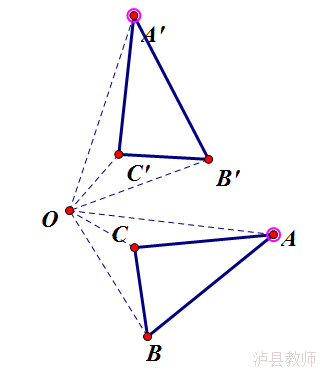
如右图，△ABC 绕O点旋转得到△A′B′C′．

小组活动探究：

（1）△ABC与△A′B′C′的形状大小有什么关系？

（2）线段OA与OA′有什么数量关系？

线段OB与OB′呢？线段OC与OC′呢？

（3）∠AOA′、∠BOB′与∠COC′有什么关系？

请大家运用刻度尺（或圆规）、量角器度量线段和有关角，并探索旋转的性质．

老师用几何画板验证它们之间的数量关系．

通过探究，你能发现图形的旋转哪些基本性质吗？

归纳：

①旋转前、后的图形______；

②对应点到__________________________；

③每一对对应点与_________所连线段的夹角等于_______．

学以致用：

例1.已知△ABC是直角三角形，∠ACB=90°，AB=5㎝，BC=3厘米，

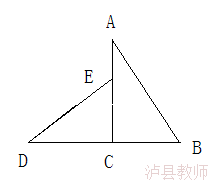
△ABC绕点C逆时针方向旋转90°后得到△DEC，则∠D=______,

∠B=______，DE=_______㎝，EC=______㎝，AE=_______㎝，

DE与AB的位置关系为__________．

例2..如图，以O为旋转中心，把△ABC顺时针旋转90°，画出旋转后的图形△A′B′C′． 

设计意图：应用旋转的性质突出重点．

【学习反思】

通过本节课的学习,你有什么收获?还有什么困惑吗?

【课后作业】

1.如图，已知△ABC 旋转得到△A′B′C′，请找出旋转中心．

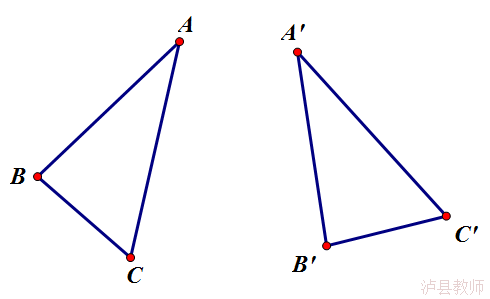
2.已知△ABC是等腰直角三角形，∠BAC=90°，∠DAE=45°，BD=2，EC=1，求DE 的长．

【板书设计】

【教学反思】

　　　本节课以学生为本，通过视频、微课、几何画板激发学生的学习热情，通过小组合作让 学生动手操作探索了旋转的性质，让学生亲自经历了知识的产生和形成．但时间还原学生导致内容没处理完．自己课前预设不够充分，以后有待加强．

../../AppData/Local/Temp/Rar$DIa7352.3182/拓.gsp