一．教学目标：

知识与技能：

1.掌握旋转地有关概念，理解旋转变换也是图形的一种基本变换.

2.经历探索图形旋转特征的过程，体验和感受图形旋转的主要特征，理解图形旋转的基本性质.

3.根据旋转地性质作出任一图形的旋转图形，并能根据所学旋转知识设计出美丽图案.

过程与方法：

1.通过观察、实际操作，理解旋转地性质，了解旋转作图的步骤及关键.

2.通过观察、操作、交流、归纳等过程，培养学生探究问题的能力、动手能力、观察能力以及与他人合作交流的能力.

情感态度：

经过对生活中旋转图形的观察、讨论、实践操作，使学生充分感知数学美，培养学生学习数学的兴趣和热爱生活的情感；通过小组合作交流活动，培养学生合作学习的意识和研究探索的精神.

二．教学重点：旋转的有关概念和旋转的基本性质。

教学难点：探索旋转的基本性质。

三．教学过程：

1.导语：我们有句古话：一寸光阴一寸金，寸金难买寸光阴。来形容时间的宝贵，而时钟则是描述时间流失的最好工具了。（多媒体展示）请同学们观察钟面上的时针演示的过程，体现了图形的哪种变换？（抽生回答）

 很好，大家可以观察时针绕着钟表的中心不停地转动，它提醒着我们一定要珍惜时间，那么就让它带领我们走入今天的旋转世界。引入课题。

2.生活中的旋转:在我们的生活中,除了时钟,还有哪些物体给大家留下了旋转的印象呢?(抽生回答).一起来欣赏下,老师给大家带来了哪些旋转的事例?(多媒体展示课件)由此可见,旋转无处不在,那么,今天就让我们一起来学习全新的图形变换----旋转.

3.新课:

一.目标1：了解旋转的定义和旋转三要素

观察下面这两幅图片中，风车的旋转有什么异同点？（多媒体展示）

归纳：图形旋转的定义：

在平面内，将              绕           转动             ，这样的图形变换称为图形的旋转。这个          称为              ，旋转的角度称为            。

强调：旋转三要素：             ，               ，                     。

二.目标2：会找旋转中心和旋转角

1.如图：△OAB绕点O按顺时针方向旋转得到△OEF，在这个旋转过程中：

⑴旋转中心是点     ，旋转角是       、       。

⑵经过旋转，点A、B分别移动到点     的位置。

⑶对应线段：OF与     ，OE与     ，EF与     。

⑷对应角：∠EOF与      ，∠E与     ，∠F与     。

2. 改变旋转中心后，如何来寻找图形中的旋转角？

如图，△ABC绕点O逆时针旋转得到△DEF，

旋转角是              ，               ，                   。

三．目标3:通过探究，得出旋转的性质

1.探究1：旋转前后的对应点到旋转中心的距离有什么数量关系？

下图中的线段A′B′是线段AB绕点O逆时针旋转90度后得到的图形。

动手操作,发现结论：                              

2.探究2：旋转前后的两个图形有什么关系？

下图的△A′B′C′是△ABC绕点O逆时针旋转90度得到的图形。

动手操作，发现结论：                        

3.探究3：对应点与旋转中心所连线段的夹角与旋转角之间有什么数量关系？

以上图为例，用量角器测∠AOA’的度数？∠AOA’=                      

由此，发现结论：                                        。

四．目标4：会用旋转的知识解决问题

问题一：下列现象中属于旋转的有(   )个

①地下水位逐年下降； ②传送带的移动；  ③方向盘的转动；

④ 水龙头开关的转动； ⑤钟摆的运动；     ⑥荡秋千运动.

A.2     B.3     C.4    D.5

问题二：钟表的分针匀速旋转一周需要60分．

（１）指出它的旋转中心；                

（２）经过20分，分针旋转了多少度？

解：

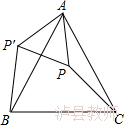
问题三：如图，△ABC为等边三角形，△AP’B是由△APC绕着点A旋转得到的。请指出：

⑴旋转中心                  ；⑵旋转角是            度；

⑶点P,C的对应点分别是           ，线段AP,PC的对应线段分别是                  ；

⑷∠PAC的对应角                    。

(对应练习)

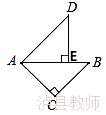
  如图，△ABC与△ADE都是等腰直角三角形，∠C和∠ADE都是直角，点E在AB上，如果△ABC经逆时针旋转后能与△ADE重合，那么旋转中心是                 ；旋转的度数                     。

五．课堂小结：

1.本节课你有什么收获？

2.本节课内容和前面学习过的什么知识可以归为一类？

六．课外拓展：

（思考）：一天,小明在做剪纸拼图游戏时,无意中,他把如图所示的两个边长是1的正方形纸片叠在一起,且点E是正方形ABCD的中心.他把正方形EFGH绕着点E转动,…… 小明思考这样一个问题:在正方形EFGH绕点E转动时,两张纸片的重叠部分面积是否一定会保持不变呢?你能帮助小明解答这一问题吗?若认为保持不变,求出它的值;否则,请简要说明理由.                

 (得胜中学郑丽)